Jak hodnotíte funkci Signum?

Rád bych pozval komunitu k účasti na pilotním experimentu. Jeho podstatou je spustit na počítači program napsaný v C++ a sdílet výsledek měření času, který vyprodukuje, porovnání rychlosti funkcí sign(x), abs(x), min(a,b) a max(a ,b) k dispozici s větvením a bez větvení. V článku vysvětlím svou motivaci, ukážu samotné funkce a na závěr navrhnu podmínky účasti v experimentu a jeho (bohužel) omezení.

Mezi programátory, zejména těmi, kteří se naučili programovat někde na konci 90. let, stále panuje silné přesvědčení, že algoritmus bez větví je lepší než algoritmus s větvemi. Často jsem viděl extrémní fanatismus ve snaze implementovat řadu jednoduchých funkcí bez větví jen proto, že si programátor myslí, že to bude efektivnější. Mezi takovými jednoduchými funkcemi jsem zatím vyzdvihl čtyři: znaménko čísla, absolutní hodnotu čísla, minimum a maximum (ve dvou verzích: pro čísla se znaménkem a bez znaménka). Pokud bude můj experiment úspěšný, použiji mnoho dalších algoritmů.

Je pravda, že bez IF je to rychlejší?

Ne, to není pravda. Přesněji řečeno, zbavení se větví může jak zvýšit rychlost, tak situaci několikrát zhoršit. Vše závisí na konkrétním stroji, na kterém bude kód spouštěn, a na kompilátoru. Jako příklad uvedu svůj starý počítač Core 2 Duo E8400 @ 3GHz – na něm všechny navrhované funkce fungují rychleji ve verzi s IF, kdy jsou data podávána spořádaně a situaci lze zvrátit, pokud data je krmen chaoticky (podrobnosti níže). Můj kompilátor je VC++ 2015, možnost kompilace /Ox.

Pojďme se blíže podívat na funkce, které navrhuji otestovat. Každá ze čtyř funkcí může být zapsána v půltuctu možností, z nichž všechny si můžete nastudovat sami pomocí odkazů [1-7] na konci článku. Všechny tyto možnosti jsem již vyzkoušel a pro každou funkci vybral dvě: klasické a některé bez větví (nejlépe dle mého měření). Pokud se můj experiment opět ukáže jako úspěšný, provedu podobné srovnání všech možností, které jsou mi známé [4-7].

Pro začátek zadám své aliasy pro datové typy a konstantu pro posun:

typedef int32_t i32; typedef uint32_t u32; typedef int8_t sign_t; const u32 SHIFT = 31;

Číselný znak – znak

Klasická verze je implementována pomocí jednoduchého schématu podmínek:

sign_t sign0 (i32 a) < if (a>0) return +1; Pokud

Nejlepší varianta bez větví vypadá takto:

sign_t sign1 (i32 a) < return (a >> SHIFT) | ((u32)(-a) >> SHIFT); >

Ano, používá posun znaménka a skutečnost, že záporná čísla jsou zakódována ve dvojkovém doplňku. Proto zde máme důležité omezení náš experiment: na svém počítači musíte mít podepsanou směnu a dodatečný kód.

Na mém procesoru je rozdíl mezi těmito dvěma funkcemi docela znatelný. Spustil jsem je na všech možných číslech z pracovního rozsahu a první fungovalo za 2,87 sekundy a druhé pouze za 3,97 s uspořádaným přísunem čísel a 13,02 vs 1,26 s chaotickým.

ČTĚTE VÍCE

Proč pijete česnekovou tinkturu?

Absolutní hodnota – abs

Zde je situace o něco lepší. První funkce s IF může vypadat takto:

u32 abs0 (i32 a)

A bez větvení vypadá nejlepší (podle mého názoru) možnost takto:

u32 abs1 (i32 a) < const i32 b = a >> SHIFT; return (a+b) ^ b; >

Provozní doba prvního je 2,29 a druhého 2,33 s uspořádaným posuvem a 12,01 vs 0,81 s chaotickým posuvem. Pozor: programátor často neví, že kompilátor sám dokáže vytvořit kód bez větví pro abs, což se bude logicky zcela shodovat s druhou možností [3]. Pokud tedy program má IF, neznamená to, že větev po kompilaci zůstane. Můj kompilátor generuje kód s větvením.

Minimum a maximum se znakem – mini a maxi

Někdo si může myslet, že klasická verze takových funkcí bude vypadat takto:

i32 mini0 (i32 a, i32 b) < return ai32 maxi0 (i32 a, i32 b) < return a>b ? a:b; >

Ve skutečnosti (a to je pro mě zcela nepochopitelné) je tato možnost jedenapůlkrát rychlejší:

i32 mini0 (i32 a, i32 b) < return a>b ? b:a; > i32 maxi0 (i32 a, i32 b)

Zjistil jsem to při porovnávání různých implementací, ale nikdy jsem nenašel konkrétní odpověď. Když jsem se podíval na výpis sestavy, zjistil jsem, že rozdíl je pouze v pořadí porovnání (porovnáváme a s b, nebo naopak). Mám podezření, že je to všechno o mikroarchitektuře procesoru. Podobně jsem si již všiml, že příkaz inc ecx funguje mnohem pomaleji než lea eax, [eax+1], což také není jasné, jak to lze vysvětlit, pokud ne zakřivením mikroarchitektury.

V mém repertoáru je pouze jedna možnost bez větví pro minimální a maximální funkce (která funguje správně pro všechna možná vstupní data):

i32 mini1 (i32 a, i32 b) < i32 d = a-b; return a - (d&(~(d^((a^b)&(d^a))) >> SHIFT)); > i32 maxi1 (i32 a, i32 b) < i32 d = a-b; return b + (d&(~(d^((a^b)&(d^a))) >> SHIFT)); >

Rozdíl je zde kolosální. První řada funkcí funguje asi 3,5 sekundy, druhá – asi 9 na sekvenční data a 2 sekundy vs 6 sekund na chaotická data. Rozdíl je v obou případech téměř trojnásobný.

Faktem je, že v architektuře x86 existuje příkaz cmovl, který umožňuje kompilátoru v prvním případě vytvořit kód bez větví. Ukazuje se tedy, že v jazyce C máme větvení, ale ve skutečnosti žádné není. Programátor, který se chce za každou cenu zbavit větví, ne vždy ví, že to překladač umí lépe než on, pokud to považuje za nutné.

Minimum a maximum bez znaménka – minu a maxu

Klasická verze se nemění, kromě nahrazení i32 u32:

u32 minu0 (u32 a, u32 b) < return a>b ? b:a; > u32 maxu0 (u32 a, u32 b)

Možnost bez větve by byla založena na jiném děsivém vzorci:

u32 minu1 (u32 a, u32 b) < u32 d = a-b; return a - (d&~(int((~a&b)|(~(a^b)&d)) >> SHIFT)); > u32 maxu1 (u32 a, u32 b) < u32 d = a-b; return b + (d&~(int((~a&b)|(~(a^b)&d)) >> SHIFT)); >

Rozdíl v rychlosti je ještě větší: pokud první možnost stále funguje 3,5 sekundy, pak druhá je již 9,5 na sekvenční data a asi 2 sekundy oproti 6 na chaotická data.

ČTĚTE VÍCE

Co mohu udělat, aby růže rostly rychleji?

Vyzývám čtenáře, aby si sami ověřili na vlastních strojích, jaký bude výsledek srovnání. Za tímto účelem byl napsán program (GitHub) (s přihlédnutím k komentářům meduzik a ivas dávám opravený program – testujeme oba. V jednom jsou data dodávána postupně, ve druhém – chaoticky). Je potřeba ho zkompilovat a spustit. Může to trvat dlouho, možná několik minut, takže buďte trpěliví. Při spuštění tohoto programu se ujistěte, že jsou v počítači zakázány další aplikace náročné na zdroje.

Po práci vypíše tabulku do STDOUT (sériový zdroj dat)

znak: 2.87 vs 3.97 abs: 2.29 vs 2.33 mini: 3.46 vs 8.93 maxi: 3.45 vs 9.10 minu: 3.45 vs 9.46 max: 3.45 vs 9.81

První sloupec obsahuje provozní dobu funkcí s IF a druhý sloupec zobrazuje provozní dobu funkcí bez větvení. Číslo se zobrazí ve STDERR, nevěnujte mu pozornost, je na kompilátoru, aby správně pochopil smyčky v programu.

Podobná tabulka pro chaotické krmení:

znak: 13.02 vs 1.26 abs: 12.01 vs 0.81 mini: 1.89 vs 5.97 maxi: 1.93 vs 6.31 minu: 1.89 vs 6.44 max: 1.92 vs 6.70

Žádám vás, abyste udělali následující: napište tyto znaky spolu s charakteristikami vašeho procesoru a názvem kompilátoru (a také možnostmi kompilace, pokud dávají smysl), jako reakci na první komentář, který uvedu. A na tento konkrétní komentář prosím nedávejte žádné další odpovědi, abyste experiment nezavrhli.

Program se nezkompiluje. To je možné, protože ne všechny kompilátory rozumí std::chrono. Také jsem možná někde překročil jazykový standard C++. Zaručuji pouze, že se kód zkompiluje ve Visual C++ 2015 a GCC 4.8.1 (od MinGW) na OS Windows 7 (64). Zkompiloval jsem přesně 32bitový kód. Zkoušel jsem se zeptat kompetentních lidí na SO, jak program vylepšit, ale zatím jsem nedostal odpověď.
Na vašem stroji nemáte posun se znaménkem nebo záporná čísla mají zastoupení ne v doplňkovém kódu – pak všechny funkce nebudou fungovat správně.
Program nebude fungovat tak, jak by měl. Je to možné. Toto je poprvé, co používám chrono a mohl jsem udělat chybu. Předtím jsem vždy měřil čas pomocí utility runexe, ale v tomto programu potřebuji univerzální metodu, která by fungovala pro většinu uživatelů.

Hacker’s Delight
Bit Twiddling Hacks
Optimalizovaná funkce abs
Funkce sign(x) – určení znaménka proměnné
Funkce abs(x) – absolutní hodnota čísla
Funkce min(a,b) a max(a,b) pro čísla se znaménkem
Funkce min(a,b) a max(a,b) pro čísla bez znaménka

Děkuji meduzikovi a ivasovi za připomenutí chaotického zdroje dat, na který jsem náhodou zapomněl.

ČTĚTE VÍCE

Jak můžete oplotit keře rybízu?

Obsah článku: (kliknutím přejdete na příslušnou část článku):

Funkce DAX SQRT
Funkce DAX POWER
Funkce DAX ABS
Funkce DAX SIGN
Funkce DAX EXP
Funkce DAX FACT
Funkce DAX LN, LOG, LOG10
Funkce DAX PI
Funkce DAX RAND a RANDBETWEEN
Funkce DAX RADIANS

Zdravím vás, drazí přátelé, Anton Buduev je s vámi. V tomto článku se podíváme na řadu nejjednodušších matematických funkcí jazyka DAX: SQRT (druhá odmocnina), POWER (umocnění), ABS (absolutní hodnota), SIGN (znak čísla), EXP (E na mocninu), FACT (faktoriál), LN , LOG, LOG10 (logaritmy), PI (Pi), RAND, RANDBETWEEN (náhodná čísla), RADIANS (radiány) v Power BI a PowerPivot.

Pro vaše pohodlí doporučuji stáhnout si „Dax Functions Reference for Power BI and Power Pivot“ ve formátu PDF.

Pokud se ve vašich vzorcích vyskytnou nějaké chyby nebo problémy a výsledky vzorců neustále neodpovídají vašim očekáváním a potřebujete pomoc, přihlaste se do bezplatného expresního kurzu „Rychlý start v jazyce funkcí a vzorců jazyka DAX pro Power BI a Power Pivot”.

Jo a ještě něco, v rámci akce do 29 máte možnost zakoupit si velký videokurz „DAX je snadné“ krok za krokem se slevou 2024 % (místo 60 10000,- za pouze 4000 XNUMX rublů)

V tomto videokurzu je jazyk DAX představen jako jednoduchý konstruktor skládající se z několika bloků, které mají svůj specifický, specifický účel. Kombinací těchto bloků různými způsoby můžete snadno vyřešit jakékoli (jednoduché nebo složité) analytické problémy pomocí návrháře vzorců DAX.

Tak využijte této příležitosti a objednejte si kurz „DAX Made Simple“ se slevou 60 % (do 29. března 2024): zjistěte více

zbývá do konce prodeje:

Funkce DAX SQRT v Power BI a Power Pivot

SQRT() je funkce druhé odmocniny čísla.

SQRT (číslo)

Kde číslo je číselná hodnota nebo sloupec obsahující číselné hodnoty.

Příklad vzorce funkce SQRT založeného na DAX:

Míra = SQRT(4)

Spuštění tohoto vzorce pomocí SQRT bude mít za následek hodnotu 2:

Funkce DAX POWER

POWER () – zvýší číslo na mocninu.

VÝKON (číslo; stupeň)

číslo – číselná hodnota nebo sloupec obsahující číselné hodnoty
stupeň – číslo požadovaného stupně

Příklad vzorce založeného na jazyce DAX pro funkci POWER:

Spuštění tohoto vzorce (2 na mocninu 2) pomocí funkce POWER bude mít za následek hodnotu 4:

Funkce DAX ABS v Power BI a Power Pivot

ABS() je funkcí absolutní hodnoty čísla. Jinými slovy, převede záporné číslo na kladné.

ABS (číslo)

Kde číslo je číselná hodnota nebo sloupec obsahující číselné hodnoty.

Příklad vzorce založeného na DAX pro funkci ABS:

Spuštění tohoto vzorce pomocí funkce ABS bude mít za následek kladnou hodnotu 5:

Funkce DAX SIGN v Power BI a Power Pivot

SIGN() – Vrátí znaménko čísla ve sloupci nebo číslo vyplývající z vyhodnocení výrazu. Hodnota 1 odpovídá kladnému číslu, hodnota 0 odpovídá nule a -1 odpovídá zápornému číslu.

SIGN (číslo)

Kde číslo je číselná hodnota nebo sloupec obsahující číselné hodnoty.

ČTĚTE VÍCE

Jak poznáte, že se jehně blíží porod?

Příklady vzorců založených na funkci DAX SIGN:

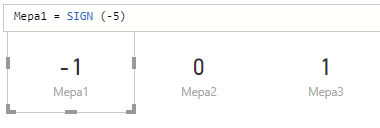
Míra 1 = znaménko (-5) Míra 2 = znaménko (0) Míra 3 = znaménko (5)

Výsledkem provádění těchto vzorců pomocí funkce SIGN budou 3 hodnoty -1 (odpovídá záporné hodnotě), 0 (odpovídá nulové hodnotě), 1 (odpovídá kladné hodnotě):

Funkce DAX EXP v Power BI a Power Pivot

EXP () – zvýší číslo E (2,71828182845904) na požadovaný výkon.

EXP (stupeň)

Kde stupeň je číselná hodnota nebo sloupec obsahující číselné hodnoty požadovaného stupně

Příklad vzorce založeného na funkci DAX EXP:

Míra = EXP (2)

Výsledkem spuštění tohoto vzorce pomocí funkce EXP bude hodnota rovna 7.39 (2,71828182845904 na mocninu 2):

Funkce DAX FACT v Power BI a Power Pivot

FACT () – faktoriál čísla (součin posloupnosti celých čísel od 1 do zadaného čísla).

FAKT (číslo)

Kde číslo je číselná hodnota nebo sloupec obsahující číselné hodnoty udávající, které číslo se má faktorializovat.

Příklad vzorce založeného na jazyce DAX pro funkci FACT:

Míra = FAKT(3)

Výsledkem provedení tohoto vzorce pomocí funkce FACT bude hodnota rovna 6 (součin řady po sobě jdoucích čísel 1*2*3):

Funkce jazyka DAX LN, LOG, LOG10 v Power BI a Power Pivot

LN() – vypočítá přirozený logaritmus čísla z konstanty E (2,71828182845904)

LOG () – vypočítá logaritmus čísla na základě základu uvedeného v parametru funkce.

LOG10() – Vypočítá logaritmus čísla se základem 10.

LN (číslo) LOG (číslo; základna) LOG10 (číslo)

Příklady vzorců založených na funkcích jazyka DAX LN, LOG a LOG10:

Měření 1 = LN (3) Měření 2 = LOG (4; 2) Měření 3 = LOG10 (7)

Výsledkem provádění těchto vzorců pomocí funkcí LN, LOG a LOG10 budou hodnoty rovné 1.1, 2, 1:

Funkce DAX PI v Power BI a Power Pivot

PI() – vrátí hodnotu Pi (3,14159265358979)

Funkce DAX RAND a RANDBETWEEN v Power BI a Power Pivot

RAND() – Vrátí náhodné číslo mezi 0 a 1 nebo rovno 0.

RANDBETWEEN () – vrací náhodné číslo mezi dvěma čísly zadanými v parametrech funkce.

RAND() RANDBETWEEN(Číslo od; Číslo do)

Kde jsou čísla „od“ a „do“ čísla, mezi kterými bude v Power BI vráceno náhodné číslo.

Příklady vzorců náhodných čísel založených na funkcích jazyka DAX RAND a RANDBETWEEN:

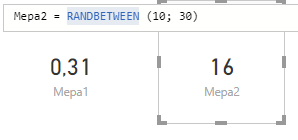
Opatření 1 = RAND() Opatření 2 = RANDBETWEEN(10; 30)

V důsledku toho RAND a RANDBETWEEN vrátily náhodná čísla 0.31 a 16:

Funkce DAX RADIANS v Power BI a Power Pivot

RADIANS() – Převádí stupně na radiány.

RADIANS (hodnota úhlu)

Kde hodnota úhlu je úhel ve stupních, který je třeba převést na radiány.

Příklad vzorce založeného na funkci DAX RADIANS:

Míra = RADIANS(4)

Spuštění tohoto vzorce pomocí funkce RADIANS bude mít za následek hodnotu 0.07:

To je vše, s analýzou matematických funkcí jazyka DAX: SQRT (druhá odmocnina), POWER (umocnění), ABS (absolutní hodnota), SIGN (znak čísla), EXP (E na mocninu), FACT (faktoriál) , LN, LOG , LOG10 (logaritmy), PI (Pi), RAND, RANDBETWEEN (náhodná čísla), RADIANS (radiány) v Power BI a PowerPivot, vše.

ČTĚTE VÍCE

Proč je nutný průzkum země?

Také připomínám, že v rámci výprodeje do 29. března 2024 máte skvělou příležitost zakoupit si velký videokurz „DAX je snadné“ krok za krokem se slevou 60 % (místo 10000 4000,- za pouze XNUMX XNUMX rublů)

Tak využijte této příležitosti a objednejte si kurz „DAX Made Simple“ se slevou 60 % (do 29. března 2024): zjistěte více

Do konce prodeje:

Ohodnoťte prosím tento článek:

Ať se vám daří, přátelé!
S pozdravem Buduev Anton.
Projekt „BI je snadné“

Pokud máte nějaké dotazy k materiálu v tomto článku, zeptejte se jich v komentářích níže. Určitě vám odpovím. A obecně tam zanechte svůj názor, budu moc rád.

Také sdílejte tento článek se svými přáteli na sociálních sítích, možná bude tento materiál pro někoho velmi užitečný.

Líbil se vám článek?
Přidejte si tento článek do záložek prohlížeče a vraťte se k němu znovu. Chcete-li to provést, stiskněte na klávesnici kombinaci kláves Ctrl + D

zbývá do konce prodeje:

Co ještě vidět/číst?

Časové funkce v jazyce DAX: ČAS, ČASOVÁ HODNOTA, HOUR, MINUTA, SECOND a NOW v Power BI a Power Pivot

Textové funkce v jazyce DAX: FORMÁT v Power BI a Power Pivot

DATESYTD, DATESQTD a DATESMTD – funkce časové inteligence DAX, které v Power BI a Power Pivot vracejí aktuální data období

Přidat komentář

zbývá do konce prodeje:

Zanecháním osobních údajů (e-mail, jméno, přihlašovací jméno) ve formulářích na stránkách tohoto webu „BI je snadné“ automaticky potvrzujete svůj souhlas s zpracování vašich osobních údajů

Tento web BI Made Easy používá k provozu soubory cookie. Pokračováním v používání webu souhlasíte s prací s těmito soubory.